We know that Convolutional Neural Networks (CNNs) are very popular when it comes to capturing specific properties of an image that are most salient for a given task. In fact, most of the research has been done in drilling down the most important spatial features in an image because it helps in reducing computational complexity and also allows the network to focus at meaningful regions of the image. If we look back at work done in the past few years, CNN models like Inception and VGG go deeper to make sure that the quality of feature maps generated from the images is improved. On the other hand, techniques such as regulating the distribution of the inputs to each layer using Batch Normalization (BN), have added stability to the learning process in deep networks. Moreover, ResNets have demonstrated that it is possible to learn considerably deeper and stronger networks with the usage of identity-based skip connections. Similarly, Highway Networks introduced a gating mechanism to regulate the flow of information along shortcut connections. Apart from these, a lot of research work has been invested in algorithmic architecture search to make sure that prominent feature maps are drawn from the input provided to the network. Recently, there has been a rise of popularity in attention and gating mechanisms that significantly reduce the model complexity by determining which region in the feature vector to focus on.
As seen above, researchers in the recent times have shown significant interest in applying attention mechanisms to improve their model’s performance by biasing the allocation of available computational resources towards the most informative components of a signal. Attention mechanisms have demonstrated their utility across many tasks including sequence learning, localisation and understanding in images, image captioning and lip reading. Attention methodologies allow us to simply incorporate itself to these applications in the form of an operator or block (following one or more layers) to represent higher-level abstractions for adaptation between modalities. For e.g. Wang et. al. in his work, introduced a powerful trunk-and-mask attention mechanism based on hourglass modules that is inserted between the intermediate stages of deep residual networks. In contrast, the technique that we are about to discuss in this post, Squeeze-and-Excitation (SE) block comprises a lightweight gating mechanism which focuses on enhancing the representational power of the network by modeling channel-wise relationships in a computationally efficient manner.
SQUEEZE-AND-EXCITATION (SE) BLOCKS
As defined in the paper, a squeeze-and-excitation block is a computational unit which can be built upon a transformation \(\textbf{F}_{tr}\) mapping an input \(\textbf{X}\) \(\in\) \(\mathbb{R}^{H^{'}*W^{'}*C^{'}}\) to feature maps \(\textbf{U} \in \mathbb{R}^{H*W*C}\).
Here, \(\textbf{F}_{tr}\) is a convolutional operator that represents the convolutional block present in our network. It can be any combination of CNN layers that extract features from the input \(\textbf{X}\).
In simple words, \(\textbf{F}_{tr}\) is responsible to convert our input \(\textbf{X}\) into feature maps \(\textbf{U}\), on top of which we build the SE block operator. By doing so, we expect the learning of convolutional features to be enhanced by explicitly modeling channel inter-dependencies, so that the network is able to increase its sensitivity to informative features which can be exploited by subsequent transformations. Consequently, we would like to provide it with access to global information and recalibrate filter responses in two steps: squeeze and excitation, before they are fed into the next transformation. The diagram below illustrates how an SE-block works upon the feature maps \(\textbf{U}\) and makes it ready for further transformation by giving emphasis to the important parts of \(\textbf{U}\) without changing its shape.
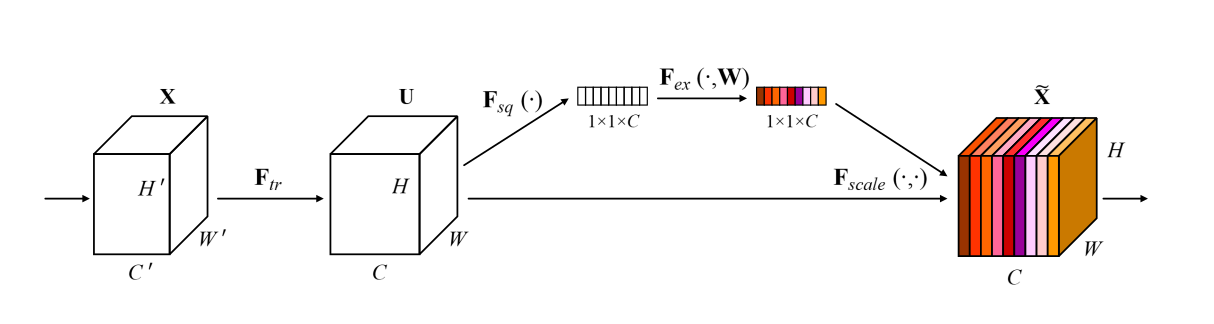
Squeeze: Global Information Embedding
To exploit the relationship between the channels in the input image, the authors propose to squeeze global spatial information into a channel descriptor (similar to how it’s done while extracting HoG feature descriptors). This is done by using global average pooling to generate channel-wise statistics. Formally, a statistic z \(\in \mathbb{R}^C\) is generated by shrinking \(\textbf{U}\) through its spatial dimensions H x W, such that the c-th element of z is calculated by:
- $z_{c}$ = \(\textbf{F}_{sq}(u_{c})\) = \(\frac{1}{H * W}\) \(\sum_{i=1}^H\) \(\sum_{j=1}^W u_{c}(i, j)\)
Here, \(\textbf{U}\) is a feature map that expresses the whole image and what SE-block tries to do is, it applies simple aggregation and global average pooling to make sure that the more expressive regions of the feature maps are revitalized.
Excitation: Adaptive Recalibration
To make use of the information aggregated in the squeeze operation, we follow it with a second operation which aims to fully capture channel-wise dependencies. This is done when we fulfil two criteria:
- First, it must be flexible, i.e. it must be capable of learning a non-linear interaction between channels
- Second, it must learn a non-mutually-exclusive relationship since we would like to ensure that multiple channels are allowed to be emphasized (rather than enforcing a one-hot activation)
To meet the above criteria, we employ a simple gating mechanism with a sigmoid activation:
- s = \(\textbf{F}_{ex}(z, W)\) = \(\sigma(g(z, W))\) = \(\sigma(W_{2}\delta(W_{1}z))\)
where,
- \(\delta\) refers to the RELU function
- \(W_{1} \in\) \(\mathbb{R}^{\frac{C}{\gamma}*C}\)
- \(W_{2} \in\) \(\mathbb{R}^{C*\frac{C}{\gamma}}\)
In order to reduce model complexity and make sure that the model generalizes well, we parameterise the gating mechanism by forming a bottleneck with two fully-connected (FC) layers around the non-linearity, i.e. a dimensionality-reduction layer with reduction ratio \(\gamma\), a RELU, and then a dimensionality-increasing layer returning to the channel dimension of the transformation output \(\textbf{U}\). The final output of the block is obtained by rescaling \(\textbf{F}\) with the activation s:
- \(\tilde x_{c}\) = \(F_{scale}(u_{c}, s_{c})\) = \(s_{c}u_{c}\)
where,
- \(\tilde X\) = [\(\tilde x_{1}\), \(\tilde x_{2}\), …, \(\tilde x_{C}\)]
- \(F_{scale}(u_{c}, s_{c})\) refers to channel-wise multiplication between the scalar \(s_{c}\) and the feature map \(u_{c}\) \(\in \mathbb{R}^{H*W}\)
The excitation operator maps the input-specific descriptor z to a set of channel weights. In this regard, SE blocks intrinsically introduce dynamics conditioned on the input, which can be regarded as a self-attention function on channels whose relationships are not confined to the local receptive field the convolutional filters are responsive to.
Conclusion
These SE blocks can be cascaded on top of each other or used alone into standard architectures like VGGNet by insertion after each convolution layer. Moreover, the flexibility of the SE block means that it can be directly applied to transformations beyond standard convolutions. The authors developed SENets by incorporating SE blocks into several examples of more complex architectures which you can find in the paper.
The github link to the repository provided in the paper is: https://github.com/hujie-frank/SENet
For PyTorch implementation of the block, you can refer to: https://github.com/moskomule/senet.pytorch
References
